| กำหนดให้ |
|
| |
z1 = z2 |
ก็ต่อเมื่อ a = c และ b = d |
|
|
|

จากหลักการดังกล่าว สรุปได้ว่า จำนวนเชิงซ้อนจะเท่ากันได้ ต้องผ่านเงื่อนไข 2 ข้อ คือ
1. ส่วนจริงเท่ากัน
2. ส่วนจินตภาพเท่ากัน
|
| |
จงหาว่าจำนวนเชิงซ้อน 4 + 5i |
และ |
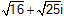 |
เท่ากันหรือไม่ |
|
|
| |
ให้ |
z1 |
= |
4 + 5i |
|
|
|
|
| |
และ |
z2 |
= |
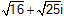 |
|
|
|
|
| |
จะได้ว่า |
Re(z1) |
= |
4 |
|
|
|
|
| |
|
Re(z2) |
= |
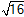 |
= |
4 |
|
|
| |
นั่นคือ |
Re(z1) |
= |
Re(z2) |
..................... |
 |
|
| |
และ |
Im(z1) |
= |
5 |
|
|
|
|
| |
|
Im(z2) |
= |
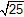 |
= |
5 |
|
|
| |
นั่นคือ |
Im(z1) |
= |
Im(z2) |
..................... |
 |
|
| |
| จาก |
 |
และ |
 |
สรุปได้ว่า |
|
| |
|
4 + 5i |
= |
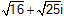 |
|
|
|
|
|

|
| |
กำหนดให้ |
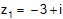 |
และ |
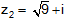 |
จงหาว่า |
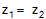 |
หรือไม่ |
|
| |
จาก |
z1 |
= |
-3 + i |
|
|
|
|
| |
และ |
z2 |
= |
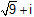 |
|
|
|
|
| |
จะได้ว่า |
Re(z1) |
= |
-3 |
|
|
|
|
| |
|
Re(z2) |
= |
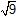 |
= |
3 |
|
|
| |
นั่นคือ |
Re(z1) |
 |
Re(z2) |
|
|
|
| |
ดังนั้น |
Re(z1) |
 |
Re(z2) |
|
|
|
|
|

|
| |
กำหนดให้ x + 2i = 3 + yi จงหาค่าของ x และ y |
|
| |
จาก |
x + 2i |
= |
3 + yi |
|
|
|
|
| |
จะได้ |
x |
= |
3 |
|
|
|
|
| |
จะได้ว่า |
y |
= |
2 |
|
|
|
|
|

|
| |
กำหนดให้ z1 = (x + y) + i และ z2 = 5 + (x - y)i จงหาค่าของ x และ y |
|
| |
จาก |
z1 |
= |
(x + y) + i |
|
|
|
|
| |
และ |
z2 |
= |
5 + (x - y)i |
|
|
|
|
| |
เนื่องจาก |
z1 |
= |
z2 |
|
|
|
|
| |
จะได้ว่า |
x + y |
= |
5 |
..................... |
 |
|
| |
นั่นคือ |
x - y |
= |
1 |
..................... |
 |
|
| |
| แก้ระบบสมการโดย |
 |
+ |
 |
|
|
| |
จะได้ |
2x |
= |
6 |
|
|
|
|
| |
|
x |
= |
3 |
|
|
|
|
| |
| แทน x = 3 ใน |
 |
เพื่อหาค่า y |
|
|
| |
จาก |
x + y |
= |
5 |
|
|
|
|
| |
จะได้ |
3 + y |
= |
5 |
|
|
|
|
| |
|
y |
= |
5 - 3 |
|
|
|
|
| |
|
|
= |
2 |
|
|
|
|
| |
ดังนั้น x = 3 และ y = 2 |
|
|

|
|