| |
ถ้า |
P(x) |
= |
 |
|
|
| |
เมื่อ |
n |
 |
I+ |
| |
| และ |
 |
เป็นจำนวนเชิงซ้อน |
|
| |
โดยที่ |
an |
 |
0 |
| |
จะเรียก |
P(x) |
ว่า |
พหุนามกำลัง n |
| |
และเรียก |
P(x) |
= |
0 ว่า สมการพหุนามกำลัง n |
|
|
 |
| |
1. |
P(x) |
= |
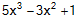 |
|
| |
|
เป็นพหุนามกำลัง 3 เพราะเลขชี้กำลังสูงสุดเป็น 3 |
|
| |
2. |
P(x) |
= |
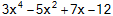 |
|
| |
|
เป็นพหุนามกำลัง 4 เพราะเลขชี้กำลังสูงสุดเป็น 4 |
|
| |
3. |
P(x) |
= |
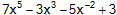 |
|
| |
|
ไม่เป็นพหุนาม เพราะมีเลขชี้กำลังติดลบ |
|
| |
4. |
P(x) |
= |
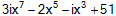 |
|
| |
|
เป็นพหุนามกำลัง 3 เพราะเลขชี้กำลังสูงสุดเป็น 3 |
|
|

|
|
| |
ถ้า |
P(x) |
= |
 |
| |
เมื่อ |
n |
 |
I+ |
| |
| และ |
 |
เป็นจำนวนเชิงซ้อน |
|
| |
โดยที่ |
an |
 |
0 |
| |
ถ้าหาร P(x) ด้วย x - c เมื่อ c เป็นจำนวนเชิงซ้อนใด ๆ แล้วจะเหลือเศษการหารเท่ากับ P(c) |
|
|
 |
| |
| จงหาเศษจากการหารพหุนาม |
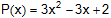 |
ด้วย x - 2 |
|
|
| |
จากโจทย์ |
P(x) |
= |
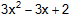 |
| |
ตัวหารคือ |
x - 2 |
|
|
| |
นั่นคือ |
c |
= |
2 |
| |
จากทฤษฎีบทเศษเหลือ จะได้ว่า เศษจากการหาร P(x) ด้วย x - 2 เท่ากับ P(2) |
| |
จาก |
P(x) |
= |
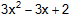 |
| |
จะได้ |
P(2) |
= |
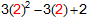 |
| |
|
|
= |
12 - 6 + 2 |
| |
|
|
= |
8 |
| |
| ดังนั้น เศษจากการหารพหุนาม |
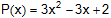 |
ด้วย x - 2 เท่ากับ 8 |
|
|
|

|
| |
| จงหาเศษจากการหารพหุนาม |
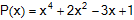 |
ด้วย x + 2 |
|
|
| |
จากโจทย์ |
P(x) |
= |
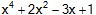 |
| |
ตัวหารคือ |
x + 2 |
= |
x - (-2) |
| |
นั่นคือ |
c |
= |
-2 |
| |
จากทฤษฎีบทเศษเหลือ จะได้ว่า เศษจากการหาร P(x) ด้วย x + 2 เท่ากับ P(-2) |
| |
จาก |
P(x) |
= |
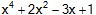 |
| |
จะได้ |
P(2) |
= |
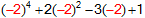 |
| |
|
|
= |
16 + 8 + 6 + 1 |
| |
|
|
= |
31 |
| |
| ดังนั้น เศษจากการหารพหุนาม |
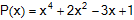 |
ด้วย x + 2 เท่ากับ 31 |
|
|
|

|
|
|